The lattice formulation of QCD was introduced by Kenneth Wilson in 1974. His pioneering work made it possible to study non-perturbative phenomena in QCD. Today there is a large community of physicists using lattice gauge theories.

In order to put the theory on the computer, one has to approximate the 4-dimensional space-time-continuum by a discrete lattice. The following picture shows an example of a curve connecting two points in two dimensions and how it could be approximated on a lattice:

Lattice QCD is based on the path integral formulation of field theories. On the lattice the theory is usually transformed from Minkowski space to Eucledian space. Nevertheless, the fundamental character of QCD is preserved.

Using this formulation of QCD it is possible to do simulations on computers using methods which are very similar to those used in statistical physics. With these techniques one can calculate correlation functions of hadronic operators and various matrix elements. Often vacuum expectation values of the following type are computed:

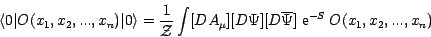
On the right hand side of this equation there is a path integral involving gauge and fermionic degrees of freedom.

Lattice QCD has in recent years proven to be a powerful tool to study non-perturbative phenomena in field theories. Recently, a review panel appointed by the European Committee for Future Accelerators (ECFA) published a report where it identified the following range of physical problems, which are amenable by numerical simulations:

• Prediction of the hadron spectrum (hadron masses, hadronic decay constants, properties of glueballs and hybrid mesons)
• Study of the running coupling, determination of quark masses, and calculation of hadronic matrix elements
• QCD thermodynamics (equation of state, value of the critical temperature, finite baryon density)
• Non-QCD Physics (electroweak physics, supersymmetric theories, chiral fermions, quantum gravity)

However, to study these problems on the lattice requires a huge amount of computer resources. This is also in future likely to be one of the main obstacles for lattice QCD. For these kind of calculations computers should be able to do a large number of FLoating Point Operations per Second (Flops). For Europe the ECFA panel recommended that several machines which have a (sustained) performance of 10 TeraFlops (=10.000.000.000.000 Flops) should become available in 2003.