When one computes observables from lattice QCD one has to solve a tremendous large amount of integrals. To handle this problem some statistical method is required. Monte Carlo methods are the standard technique to deal with this problem.

As an easy example we demonstrate the numerical solution of the following integral, where the exact analytic result is known:

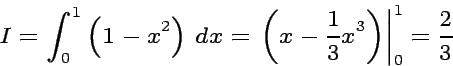
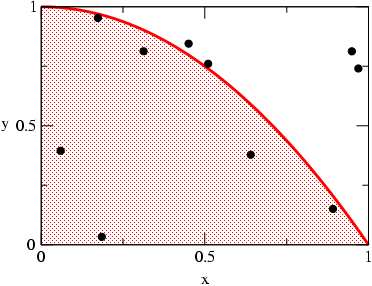
The integral is equal to the size of the red area shown in the picture below. If we distribute 10 points randomly in the surrounding square of size one, we expect the numbers of points within the red area to be proportional to the size of the area. Therefore, a first numerical estimate of the integral would be I = 6/10 = 0.6.

After iterating this procedure up to 100 points I = 0.67, which is already much closer to the real answer I=2/3.

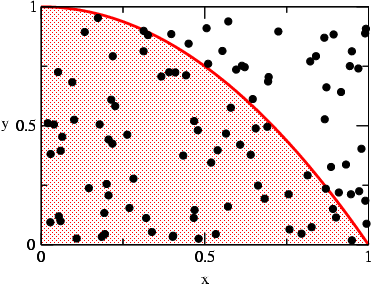
For a simple integral like here this is not a very good (i.e. a slowly converging) method . But for the integrals to be solved in lattice QCD it is the only known efficient method.